Lagrangian problems, inclined planes

Problem:

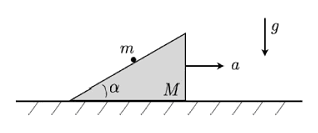
A wedge of mass M rests on a horizontal frictionless surface.  A point mass m is placed on the wedge, whose surface is also frictionless.  Find the horizontal acceleration a of the wedge.

Solution:

• Concepts:
  Lagrangian Mechanics
• Reasoning:
  All forces, except the forces of constraint, are derivable from a potential.  The Lagrangian formalism is well suited for such a system because we do not have to solve for the forces of constraint or explicitly eliminate them from the equations of motion.
• Details of the calculation:
  
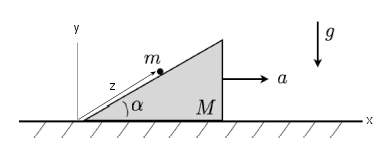
  L = T - U.
  T = T_wedge + T_m = ½M(dx₂/dt)² + ½m[(dx₁/dt)² + (dy₁/dt)²].  U = mgy₁.
  Constraints: x₁ = x₂ + z cosα,  y₁ = z sinα.
  L = ½m[(dx₂/dt)² + (dz/dt)² + 2(dx₂/dt)(dz/dt) cosα] + ½M(dx₂/dt)² - mgz sinα.
  The equations of motion are obtained from d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = 0.
  for q₁ = x₂ and q₂ = z.
  (m + M)(d²x₂/dt²) + m(d²z/dt²) cosα = 0.
  The horizontal position of the CM does not change.
  m(d²z/dt²) + m(d²x₂/dt²)cosα + mg sinα = 0.
  Combining:
  a = d²x₂/dt² = mg cosα sinα/(M + m - m cos²α) = mg cosα sinα/(M + m sin²α).
  
  You can also work from Newton's laws.  The equations of motion then are
  -Nsinα = m(d²x₁/dt²) ,
  Nsinα = M(d²x₂/dt²), 
  -mg + Ncosα = m(d²y₁/dt²),
  with x₁ = x₂ + z cosα,  y₁ = z sinα.
  We have to solve for d²x₂/dt². Using Newton's laws, we have to explicitly eliminate the force of constraint N.
  From the first two equations:
  m(d²x₁/dt²) + M(d²x₂/dt²) = (m + M)(d²x₂/dt²) + m(d²z/dt²) cosα = 0.
  From the third equation:
  N = [m(d²z/dt²)sinα + mg]/cosα.
  Insert this back into the second equation:
  [m(d²z/dt²)sin²α + mgsinα]/cosα = M(d²x₂/dt²).
  [-(m + M)(d²x₂/dt²)sin²α/cosα  + mgsinα]/cosα = M(d²x₂/dt²).
  mg sinα cosα = M(d²x₂/dt²)cos²α + (m + M)(d²x₂/dt²)sin²α
  mg sinα cosα = (d²x₂/dt²) (M + m sin²α).
  a = d²x₂/dt² =  mg cosα sinα/(M + m sin²α).

Problem:

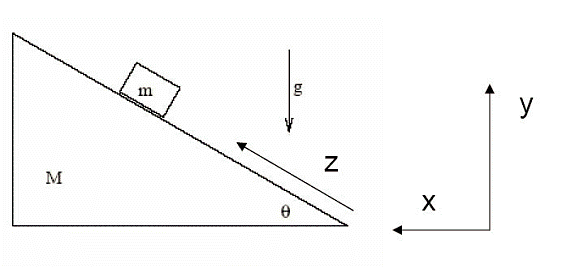
A wedge of mass M = 4.5 kg sits on a horizontal surface.  Another mass m = 2.3 kg sits on the sloping side of the wedge.  The incline is at an angle θ = 31.7 degrees with respect to the horizontal, and g = 9.8 m/s.  All surfaces are frictionless.  The mass m is released from rest on mass M, which is also initially at rest.  Use Lagrangian mechanics to determine the vector values of the accelerations of both M and m once the mass is released.

Solution:

• Concepts:
  Lagrangian Mechanics
• Reasoning:
  We are asked to use Lagrangian Mechanics to solve the problem.
• Details of the calculation:
  L = T - U.
  T = T_wedge + T_m = ½M(dx₂/dt)² + ½m[(dx₁/dt)² + (dy₁/dt)²].  U = mgy₁.
  Constraints: x₁ = x₂ + z cosθ,  y₁ = z sinθ.
  L = ½ m[(dx₂/dt)² + (dz/dt)² + 2(dx₂/dt)(dz/dt) cosθ] + ½M(dx₂/dt)² - mgz sinθ.
  The equations of motion are obtained from  d/dt(∂L/∂(dq/dt)) -  ∂L/∂q = 0, for q = x₂ and q = z.
  (m + M)(d²x₂/dt²) + m(d²z/dt²) cosθ = 0,
  m(d²z/dt²) + m(d²x₂/dt²) cosθ + mg sinθ = 0.
  d²x₂/dt² = (mg cosθ sinθ)/(M + m - m cos²θ).
  Inserting the numerical values we have:
  d²x₂/dt² = 1.9624 m/s²,
  d²z/dt² = -6.82 m/s²,
  d²x₁/dt² = -3.85 m/s²,
  d²y₁/dt² = -3.58 m/s².

Problem:

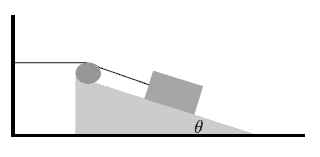
The system, shown in the diagram, consists of a wedge placed on a horizontal surface and a block connected to a string that passes over a massless pulley attached to the wedge.  The other end of the string is attached to the wall so that the string is horizontal between the wall and the pulley, and parallel to the inclined surface between the pulley and the block. The wedge and the block have equal masses m.  The angle θ is given.  When the system is released from rest the block begins to slide along the inclined surface of the wedge.  Neglecting all friction, find the acceleration of the wedge.

Solution:

• Concepts:
  Lagrangian mechanic
• Reasoning:
  The Lagrangian method often simplifies the treatment of systems with holonomic constraints.
• Details of the calculation:
  Let the string have length L.  Let x be the coordinate of the point where the string touches the pulley.
  Then coordinates of the point where the string attaches to the block are
  x' = x + (L - x)cosθ, y' = h - (L - x)sinθ,  where h is the height of the point where the string attaches to the wall.
  The kinetic energy of the system is T = ½ mv_x² + ½ m(v_x'² + v_y'²) = ½ m v_x² (3 - 2cosθ).
  The potential energy is U = m g x sinθ + constant.
  L = ½ m v_x² (3 - 2cosθ) - m g x sinθ
  ∂L/∂v_x = mv_x(3 - 2cosθ),  d/dt(∂L/∂v_x) = ma_x(3 + 2cosθ),  ∂L/∂x = - m g sinθ.
  a_x = - g sinθ/(3 - 2cosθ).

Problem:

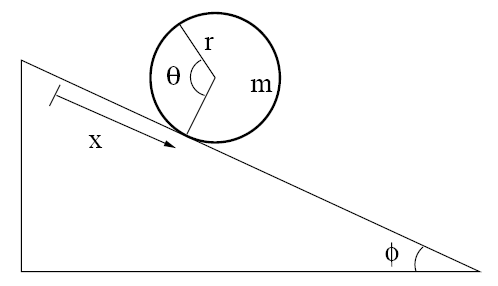
Consider a hoop of mass m and radius r rolling without slipping down an incline.
(a)  Determine the Lagrangian L(x, dx/dt) of this one-degree-of-freedom system.  Derive from it the Lagrange equation and its solution for initial condition x₀ = 0, dx/dt|₀ = 0.
(b)  Determine the alternative Lagrangian L(x, dx/dt, θ, dθ/dt)  and the holonomic constraint f(x, θ) = 0 that must accompany it.  Derive the associated three equations of motion for the two unknown dynamical variables x and θ, and the undetermined Lagrange multiplier λ.  Solve these equations for the same initial conditions as in (a) and determine the static frictional force of constraint between the hoop and the incline.

Solution:

• Concepts:
  Lagrange's Equations, Lagrange multipliers
• Reasoning:
  In part (a) we use the constraint of rolling to eliminate the coordinate θ.
  In part (b) we are asked to use the method of Lagrange multipliers.  Then the equations of motion are be obtained from
  d/dt(∂L/∂(dq_k/dt)) -  ∂L/∂q_k = ∑_lλ_la_lk,  Σ_k a_lk dq_k + a_lt dt =  0.
• Details of the calculation:
  (a)  L = T - U.
  T = (m/2)v² + (I/2)ω².  v = dx/dt,  ω = dθ/dt = v/r, I = mr², U = -mgxsinΦ.
  L = m(dx/dt)² + mgxsinΦ.
  ∂L/∂v = 2mdx/dt,  (d/dt)∂L/∂v = 2md²x/dt², ∂L/∂x = mgsinΦ.
  d²x/dt² = (g/2)sinΦ.  a_x = (g/2)sinΦ, v_x = (gt/2)sinΦ, x = (gt²/4)sinΦ.
  (b)  L = (m/2)(dx/dt)² + (mr²/2)(dθ/dt)² + mgxsinΦ.
  Constraint: dθ = dx/r,  dx - rdθ  = 0.
  We have two coordinates, x and θ, and one equation of constraint, dx - rdθ  = 0, which must be cast into the form λ₁∑a_1k dq_k = 0,  λ₁(a_1x dx + a_1θ dθ) = 0.  Therefore a_1x = 1, a_1θ  =  -r.
  ∂L/∂v = mdx/dt,  (d/dt)∂L/∂v = md²x/dt², ∂L/∂x = mgsinΦ.
  ∂L/∂ω = mr²dθ/dt,  (d/dt)∂L/∂ω = mr²d²θ/dt², ∂L/∂θ = 0.
  md²x/dt² - mgsinΦ = λ,  mr²d²θ/dt² = -rλ,   d²x/dt² = rd²θ/dt².
  3 equations, 3 unknowns.
  d²x/dt² = (g/2)sinΦ, d²θ/dt² = (g/(2r))sinΦ,  λ = -(mg/2)sinΦ.
  Here λ = F_x is the force of constraint associated with the coordinate x.  It is the static frictional force of constraint between the hoop and the incline.
  The generalized force of constraint associated with the coordinate θ is -rλ =  r(mg/2)sinΦ.  It is the torque acting on the hoop, pointing into the page.

Problem:

Two spheres are of the same radius R and mass M, but one is solid and the other is a hollow shell (of negligible thickness).  Both spheres roll (without sliding) down a ramp of incline θ.
(a)  Which sphere will have the greater acceleration down the ramp?
(b)  Determine the Lagrangian for the motion of the sphere and derive the equation of motion for both cases.

Solution:

• Concepts:
  Lagrange's Equations
• Reasoning:
  All forces except the forces of constraint are derivable from a potential.  The Lagrangian formalism is well suited for such a system.  We are asked to derive Lagrange's equation of motion.
• Details of the calculation:
  (a)  We have a conservative system.  Potential energy is converted into rotational and translational kinetic energy ½Iω² + ½Mv² with v = ωR.  The moment of inertia of the solid sphere I = (2/5)MR² is smaller than the moment of inertia of the thin spherical shell I = (2/3)MR², so the solid sphere will have the greater linear acceleration down the ramp.
  (b)  Set up a coordinate system:
  

  L = T - U.  T = ½(I/R² + M)(dx/dt)²,  U = Mgxsinθ.
  L = ½(I/R² + M)(dx/dt)² - Mgxsinθ.
  Equation of motion: (d/dt)(∂L/∂v) - ∂L/∂x = 0, with v = dx/dt.
  (I/R² + M)d²x/dt² + Mgsinθ = 0.
  a =  d²x/dt² = (M/(I/R² + M))gsinθ.
  For the solid sphere:  a = (5/7) gsinθ.
  For the spherical shell:  a = (3/5) gsinθ.